赫夫曼树以及应用

介绍

当用 n 个结点（都做叶子结点且都有各自的权值）试图构建一棵树时，如果构建的这棵树的带权路径长度最小，称这棵树为“最优二叉树”，有时也叫“赫夫曼树”或者“哈夫曼树”。
在构建哈弗曼树时，要使树的带权路径长度最小，只需要遵循一个原则，那就是：权重越大的结点离树根越近。在图 1 中，因为结点 a 的权值最大，所以理应直接作为根结点的孩子结点。

如下图就是：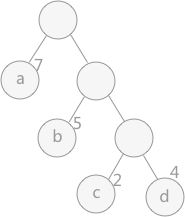

关键词

路径：在一棵树中，一个结点到另一个结点之间的通路，称为路径。
路径长度：在一条路径中，每经过一个结点，路径长度都要加 1 。例如在一棵树中，规定根结点所在层数为1层，那么从根结点到第 i 层结点的路径长度为 i - 1 。
结点的权：给每一个结点赋予一个新的数值，被称为这个结点的权。
结点的带权路径长度：指的是从根结点到该结点之间的路径长度与该结点的权的乘积。
WPL：树的带权路径长度为树中所有叶子结点的带权路径长度之和。

构建最优二叉树

对于给定的有各自权值的 n 个结点：
1.在 n 个权值中选出两个最小的权值，对应的两个结点组成一个新的结点，两个结点作为新结点的孩子，且新的结点权值为左右孩子权值的和。
2.在原有的 n 个结点中删除那两个最小的权值，同时将新的结点加入到 n–2 个权值的行列中，以此类推。
3.重复 1 和 2 ，直到所以的结点构建成了一棵二叉树为止，这棵树就是哈夫曼树。

java代码

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;

public class HuffmanTree {

    public static void main(String[] args) {
        HuffmanTree tree = new HuffmanTree();
        Integer[] array = {1,5,3,2,7,9,6,4,8,15,10,12,13,11,14};
        Node root = tree.createTree(array);
        tree.inTraverse(root);
    }

    public Node createTree(Integer[] array){
        if (array == null || array.length == 0){
            return null;
        }
        List<Node> nodeList = new ArrayList<>();
        Node node;
        for (Integer item : array){
            node = new Node();
            node.value = item;
            nodeList.add(node);
        }
        while (nodeList.size()>1){
            Collections.sort(nodeList);
            Node newNode =  new Node();
            newNode.leftChild = nodeList.get(0);
            newNode.rightChild = nodeList.get(1);
            newNode.value = nodeList.get(0).value + nodeList.get(1).value;
            nodeList.remove(0);
            nodeList.remove(0);
            nodeList.add(newNode);
        }
        return nodeList.get(0);
    }

    public void inTraverse(Node node){
        System.out.println(node.value);
        if (node.leftChild!=null){
            inTraverse(node.leftChild);
        }
        if (node.rightChild!=null){
            inTraverse(node.rightChild);
        }
    }

    class Node implements Comparable<Node>{

        Integer value;
        Node leftChild;
        Node rightChild;

        @Override
        public int compareTo(Node o) {
            return this.value - o.value;
        }

        @Override
        public String toString() {
            return "node="+this.value;
        }
    }
}

应用场景

这个技术普遍用来构建哈弗曼编码，是一种编码方式，可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现
概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）。主要应用在数据压缩，加密
解密等场合。

为什么要用哈弗曼编码？因为我们在使用普通编码的时候，一个编码可能会出现歧义，所以我们需要一个没有歧义的编码，并且要让长度尽可能的少。

使用哈弗曼编码进行压缩，是一种无损失压缩，压缩率在50%左右。

哈弗曼编码数据压缩java代码

import java.util.*;

public class HuffmanCode{

    static Map<Byte, String> map = new HashMap<>();

    HuffmanTree tree = new HuffmanTree();

    public static void main(String[] args) {
        String str = "i dokjhjknkjng vjkllskjcas asdfjasd askdj askdfj asjf";
        byte[] array = str.getBytes();
        HuffmanCode code = new HuffmanCode();
        Node root = code.tree.createTree(array);
        code.getCode(root, "",new StringBuilder());
        System.out.println(map);
    }

    public String getZip(byte[] array){
        StringBuilder builder = new StringBuilder();
        for (byte item : array){
            builder.append(map.get(item));
        }
        return builder.toString();
    }

    /**
     * 将获得的哈夫曼编码放入map里面
     * @param node
     * @param code
     * @param builder
     */
    public void getCode(Node node,String code, StringBuilder builder){
        builder.append(code);
        if (node.leftChild != null){
            getCode(node.leftChild, "0", new StringBuilder(builder));
        }
        if (node.rightChild != null){
            getCode(node.rightChild, "1", new StringBuilder(builder));
        }
        if (node.value != null){
            map.put(node.value, builder.toString());
            return;
        }
    }

    class Node implements Comparable<Node>{

        Integer weight;
        Byte value;
        Node leftChild;
        Node rightChild;

        @Override
        public int compareTo(Node o) {
            return this.weight - o.weight;
        }

        @Override
        public String toString() {
            return new String("char:"+this.value+"weight:"+this.weight);
        }
    }

    class HuffmanTree{
        Map<Byte, Integer> map;

        public HuffmanCode.Node createTree(byte[] array){
            if (array.length==0 || array == null){
                return null;
            }
            calculateWeight(array);
            List<HuffmanCode.Node> nodeList = createNode();
            while (nodeList.size() > 1){
                Collections.sort(nodeList);
                System.out.println(nodeList);
                HuffmanCode.Node node = new HuffmanCode.Node();
                node.weight = nodeList.get(0).weight + nodeList.get(1).weight;
                node.leftChild = nodeList.get(0);
                node.rightChild = nodeList.get(1);
                nodeList.remove(nodeList.get(0));
                nodeList.remove(nodeList.get(0));
                nodeList.add(node);
            }
            return nodeList.get(0);
        }

        public List<HuffmanCode.Node> createNode(){
            if (map == null){
                return null;
            }
            List<HuffmanCode.Node> nodeList = new ArrayList<>();
            for (Map.Entry<Byte, Integer> item : map.entrySet()){
                HuffmanCode.Node node = new HuffmanCode.Node();
                node.value = item.getKey();
                node.weight = item.getValue();
                nodeList.add(node);
            }
            return nodeList;
        }

        public void calculateWeight(byte[] array){
            if (array.length==0 || array == null){
                return;
            }
            map = new HashMap<>();
            for (Byte item : array){
                if (map.get(item) == null){
                    map.put(item, 1);
                }else {
                    map.put(item, map.get(item) + 1);
                }
            }
        }
    }

}